1. 案例场景

假设你是肯德基的门店运营负责人，某天，你们决定在某家分店（称为 A 店）推出买一送一的促销活动。你想评估这项促销活动的效果，看看它是否提高了这家分店的销售额。

这个评价问题在于，你只有一家分店进行了促销活动，其他的分店都没有进行相同的促销。你无法直接比较 A 店的销售额和没有进行促销的分店的销售额，因为这些分店可能本身就存在很多差异，比如地理位置、人流量等因素。

但通过使用其他分店（控制组）的数据来构建一个“虚拟”的对照组，这个虚拟的对照组在没有促销的情况下表现得和 A 店相似。通过比较促销之后实际的 A 店和这个虚拟对照组的业绩，就可以评估促销活动的效果。

• 收集 A 店在促销活动前后的一段时间内的销售数据。
• 收集其他分店在同一时间段内的销售数据。
• 选择一些影响销售额的关键特征，比如每天的顾客数量、人均消费额等。

通过对其他分店的特征进行加权平均，构建一个“合成”分店，使其在促销活动开始之前的特征与 A 店尽可能相似。例如，假设你选择了三家分店 B、C 和 D，它们在促销开始前的特征分别是：

• B 店：顾客数量 100 人，人均消费额 20 元；
• C 店：顾客数量 150 人，人均消费额 25 元；
• D 店：顾客数量 200 人，人均消费额 30 元。

如果你发现 A 店在促销开始前的特征是顾客数量 150 人，人均消费额 25 元，那么你可以给 B、C、D 店分配权重，使得加权平均后的特征与 A 店相近。比如，权重可能是 B 店 20%，C 店 60%，D 店 20%。

实际和合成控制组有这样的比较效果：

• 促销活动前 A 店销售额序列和合成组（由其他分店加权平均得到）销售额序列基本一致。
• 活动后，比较 A 店的实际销售额与合成控制组的预测销售额。
• 如果 A 店的实际销售额显著高于合成控制组的预测销售额，那么可以认为促销活动是有效的。

以上是一个简单的原理说明，下面从详细的数学理论做完整推导和扩展。

2. 数学原理

以上方法被称为合成控制法（Synthetic Control Method, 简称 SCM），它是一种用于评估政策干预效果的统计方法，特别适用于只有一个或少数几个单位接受了干预的情况。这种方法通过构建一个“合成控制”组来模拟未接受干预的单位，从而估计干预的效果。

假设我们有 $J+1$ 个单元，其中第 1 个单元是处理单元，其余 $J$ 个单元是对照单元。我们观测到每个单元在 $T$ 个时间段内的结果变量 $Y$ 和协变量 $X$。

对于协变量 $X_i$，我们可以定义一个权重矩阵 $V$ 来反映不同协变量向量的重要性。假设 $X_i$ 包含了 $k$ 个向量。$i$ 是列，$k$ 是行，则 $V$ 可以是一个 $k \times k$ 的对角矩阵，其中对角线上的元素代表每个（行）向量的相对重要性。

定义：

• $Y_{it}$：单元 $i$ 在时间 $t$ 的结果变量。
• $X_{i}$：单元 $i$ 的协变量。
• $V_{k \times k}$：$X_{i}$ 中 $k$ 个向量的权重。

换一个经典的美国加州控烟效果的数据集来说明，$X_i$ 的示例数据如下：

$X_i$ 的列向量则是美国各个州的表现，行向量有 7 个，分别对应的是

1. 在 1970 年至 1988 年之间的平均数：收入的对数（lnicome）、消费的啤酒量（beer）、15 至 24 岁的人口比例、香烟售卖均价。
2. 以及重点关注的 1975、1980、1988 年香烟售卖量。

这里需要注意的一点是，由于研究目的或者数据记录缺失等问题，$X_i$ 很可能不是一个面板数据。

$Y_{jt}$ 表示的是各个州在 1970 至 2000 年之间的每年香烟消费量，这是我们最关注部分。示例数据如下：

合成控制组的构建：

• 选择一组权重 $\mathbf{w} = (w_2, w_3, \ldots, w_{J+1})$，使得 $\sum_{j=2}^{J+1} w_j = 1$ 且 $w_j \geq 0$。

• 构建合成控制组的协变量向量 $\hat{X}_1$：

  $$\hat{X}_1 = \sum_{j=2}^{J+1} w_j X_j$$

• 构建合成控制组的结果变量 $\hat{Y}_{1t}$：

  $$\hat{Y}_{1t} = \sum_{j=2}^{J+1} w_j Y_{jt}$$

这时候我们拥有两个损失（在处理前的时间段 $T$ 内）：

$LOSS^Y = \sum_{t=1}^{T} \left( Y_{1t} - \sum_{j=2}^{J+1} w_j Y_{jt} \right)^2$

$LOSS^X = (X_1 - \sum_{j=2}^{J+1} w_j X_j)' V (X_1 - \sum_{j=2}^{J+1} w_j X_j)$

如果有一个 $\mathbf{w}$ 能够使得 $LOSS^Y, LOSS^X$ 都能够最小化。这样我们就找到了一个合成州，它的协变量、结果变量均和处理单元表现的非常接近。那么，单元在处理后的因果效应 $\tau_{1t}$ 定义为处理单元和合成控制组在处理后的结果变量之差：

注意，这里 $Y_i$ 的行向量权重被认定为 1，因为它们是同样属性的内容，都是香烟的年消费量，权重相等。但 $X_i$ 的行向量属性不同，它们有些是处理前时间内的汇总数据，有些则是具体某年的 $Y_i$（业务表达为起始初始值相同）。这些因素对 $Y_i$ 的解释性也不同，因此权重阵 $V$ 被考虑了。这也合成控制法的核心思想之一。

在实际应用中，协变量 $X_i$ 通常包括一些在处理前已知的、与结果变量相关的特征。通过将这些协变量纳入合成控制组的构建过程中，可以提高合成控制组的合理程度，从而更准确地估计因果效应。

3. 嵌套最优化

前文描述是一个非常粗略的解释，合成控制法的的实际优化目标是：

$\min_{V} \left(Z_1 - Z_0 W^{(V)}\right)^{T} \left(Z_1 - Z_0 W^{(V)}\right)$

• $V$ 是 $k$ 个协变量向量的权重。
• $W^{(V)}$ 是合成控制组（$J$ 个对照单元）的权重向量，基于 $X_1$ 和 $X_0$ 求解。$X_1$ 和 $X_0$ 分别是，处理组协变量和 $J$ 个对照组协变量。
• $Z_1$ 和 $Z_0$ 分别是，在处理时间段 $T$ 内，处理组结果变量和 $J$ 个对照组结果变量。

$V$ 和 $W$ 是需要优化两个参数。

请注意，合成控制法是本质是用 $V$ 找合成结果变量，最小化 $LOSS^{Y}$。$W$ 只是顺道求解出来的中间结果，$W$ 并不被直接求解。

这问题的解法稍有一点绕，涉及到嵌套最优化：我们需要先优化一个目标函数，然后将优化结果用于另一个目标函数的优化。具体来说，可以分解为以下两个步骤：

1. 优化 $W$ 使得 $\left|X_1 - X_0 W\right|_V$ 最小化。
2. 使用前一步得到的 $W$ 来优化 $V$ 使得 $\left(Z_1 - Z_0 W^{(V)}\right)^{T} \left(Z_1 - Z_0 W^{(V)}\right)$ 最小化。

3.1. 第一步：优化 $W$

首先，我们需要最小化 $\left|X_1 - X_0 W\right|_V$，即：

$\left|X_1 - X_0 W\right|_V^2 = \left(X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W\right)$

可以通过求解以下方程来找到 $W$：

$\min_W \left(X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W\right) = \min_W (X_1^T V X_1 - 2 X_1^T V X_0 W + W^T X_0^T V X_0 W)$

设 $A = X_0^{T} V X_0$ 和 $B = X_0^{T} V X_1$，则问题变为：

$\min_W (X_1^{T} V X_1 - 2 B^{T} W + W^{T} A W)$

对 $W$ 求导并令其等于零。

由于 $X_1^{T} V X_1$ 不依赖于 $W$，因此求导过程等价于：

得到：

$2 A W - 2 B = 0$ $A W = B$ $W = A^{-1} B$

但这个方法有个弊端，一旦 $A$ 是奇异矩阵（singular matrix），则 $A^{-1}$无解。所以需要转化一下思路。同上文描述，由于 $X_1^T V X_1$ 不依赖于 $W$，因此

$\min_W \left(X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W\right)$

等价于

$\min_W (W^T X_0^T V X_0 W - 2 X_1^T V X_0 W)$

假如我们设:

• $H = X_0^T V X_0$
• $c = -2 X_1^T V X_0$

是一个二次规划问题:

$w^T H w + c^T w$

同时考虑到 $w$ 限制条件，即

$X_0$ 和 $X_1$ 是常数阵，任意给定 $V$，都可以求得符合条件的 $W$，使得 $\left|X_1 - X_0 W\right|_V^2$ 最小。

3.2. 第二步：优化 $V$

使用第一步中优化得到的 $W$，接着最小化：

$\left(Z_1 - Z_0 W^{(V)}\right)^{T} \left(Z_1 - Z_0 W^{(V)}\right)$

想象一下，$W^{(V)}$ 是 $V$ 的函数，任意个 $V$ 就可以得到 $W$，并计算出上式的 loss，所以这是一个关于 $V$ 的优化问题（嵌套了一层 $W$）。我们需要找到 $V$ 使得上述表达式最小化。

到这一步就容易了，可以借助通用梯度下降法来求解。合成控制法的这两个步骤很巧妙，通过嵌套的方式同时保证了 $Loss^Y, Loss^X$ 均为最小。

当然，将最优的 $V$ 求解出来后，还需要重新执行一遍第一步，以获得最优 $W$。

3.3. 系数和模型表现

使用前述方式计算各个参数，$V$ 的结果为：

      v.names    v
1    lnincome 0.15
2        beer 0.17
3   age15to24 0.07
4    retprice 0.01
5 cigsale1975 0.39
6 cigsale1980 0.14
7 cigsale1988 0.08

$W$ 的结果为：

      state_name    w
1       Colorado 0.02
2    Connecticut 0.01
3          Idaho 0.07
4       Illinois 0.01
5           Iowa 0.01
6         Kansas 0.01
7      Minnesota 0.01
8        Montana 0.29
9       Nebraska 0.01
10        Nevada 0.18
11 New Hampshire 0.01
12  North Dakota 0.01
13  South Dakota 0.01
14         Texas 0.01
15          Utah 0.29
16     Wisconsin 0.01
17       Wyoming 0.01

合成的 $\hat{Y}_{1t}$ 同原始 $Y_{1t}$ 的对比曲线如下图所示：

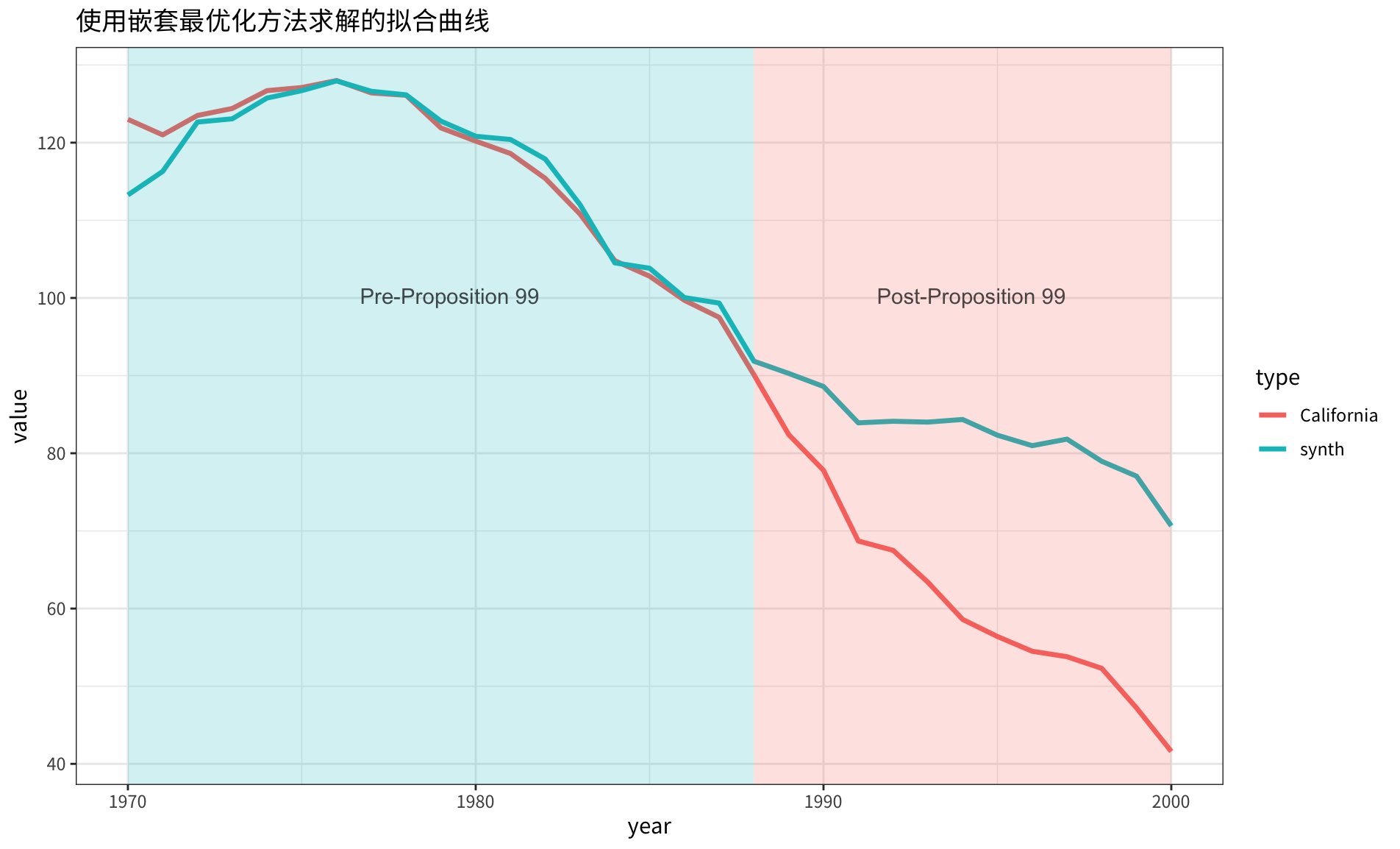
4. 重定义损失函数

合成控制法通过嵌套最优化的方法，得到两个参数 $W, V$ 的最优值。但实际上，大家仔细想想：难道我们不清楚协变量中各个向量的重要性吗？用模型算一个最优的 $V$ 你敢直接用吗？业务解释性如何？

我们可否用一个更加通用的损失函数，能够同时考虑结果变量和协变量？答案显然是可以的！一旦通过某种手段求解了 $V$，简单的将 $LOSS^X$ 和 $LOSS^Y$ 加起来就是解法之一。下面我们看看这个方法的可行性和效果。

首先是协变量的权重 $V$ 的求解，有几种思路可供参考：

1. 基于先验业务，为每个协变量赋予一个权重，比如 AHP 专家评分法。
2. 如果 $X_i$ 同 $Y_i$ 一样是面板数据，那么基于机器学习算法，估计 $X_i$ 各个向量的对 $Y_i$ 的影响，影响权重即为协变量的重要性。

4.1. 机器学习估计 $V$

从数据出发，什么因素会影响到各州的香烟消费量？$X_i$ 中 4 个要素：收入的对数（lnicome）、消费的啤酒量（beer）、15 至 24 岁的人口比例（age15to24）、香烟售卖均价（retprice）。当然，各州的本身，它们也是影响香烟消费量的关键因素。

数据可以构建这样（各州本身被转换为了 0,1 特征）：

各位看官看到这里，应该有感觉了，有太多机器学习方法可以获得每个特征的重要性。比如通过随机森林找到各个特征的重要程度，去除州的影响之后，测算得到 $V$ 为：

这个权重同我们的常识相对一致：刨除州本身的影响后，最大影响因素依次是香烟价格、15-24 岁人口、收入的对数、啤酒销量。需要注意的是，这种求解方法只适应于协变量 $X_i$ 是面板数据，像原始论文那样，把 1975、1980、1988 年的香烟销售量同样作为协变量，这个方法不适用。

4.2. 合并损失函数

只要 $V$ 就绪，就可以优化以下损失函数以求解 $w$。这个损失函数由 $LOSS^X$ 和 $LOSS^Y$ 合并而得。

其中，$\lambda$ 是一个权重，用于平衡结果变量和协变量的拟合程度。是更倾向于结果变量一致，还是协变量。

注意：为了保证 $\lambda$ 权重有效，结果变量和协变量需要归一化，比如这里利用的是“单位向量归一化”方法：

4.3. 系数和模型表现

$\lambda = 1$ 时，结果变量和协变量拟合程度的权重相等。

在 $V$ 的权重控制下，后两项的相似程度更接近，对业务解释显然更加友好。

而且 $W$ 的不为 0 的数量居然还更少（合成州数量少）！

           name    w
1      Colorado 0.03
2   Connecticut 0.10
3       Montana 0.24
4        Nevada 0.21
5 New Hampshire 0.04
6          Utah 0.38

合成的 $\hat{Y}_{1t}$ 同原始 $Y_{1t}$ 的对比曲线如下图所示：

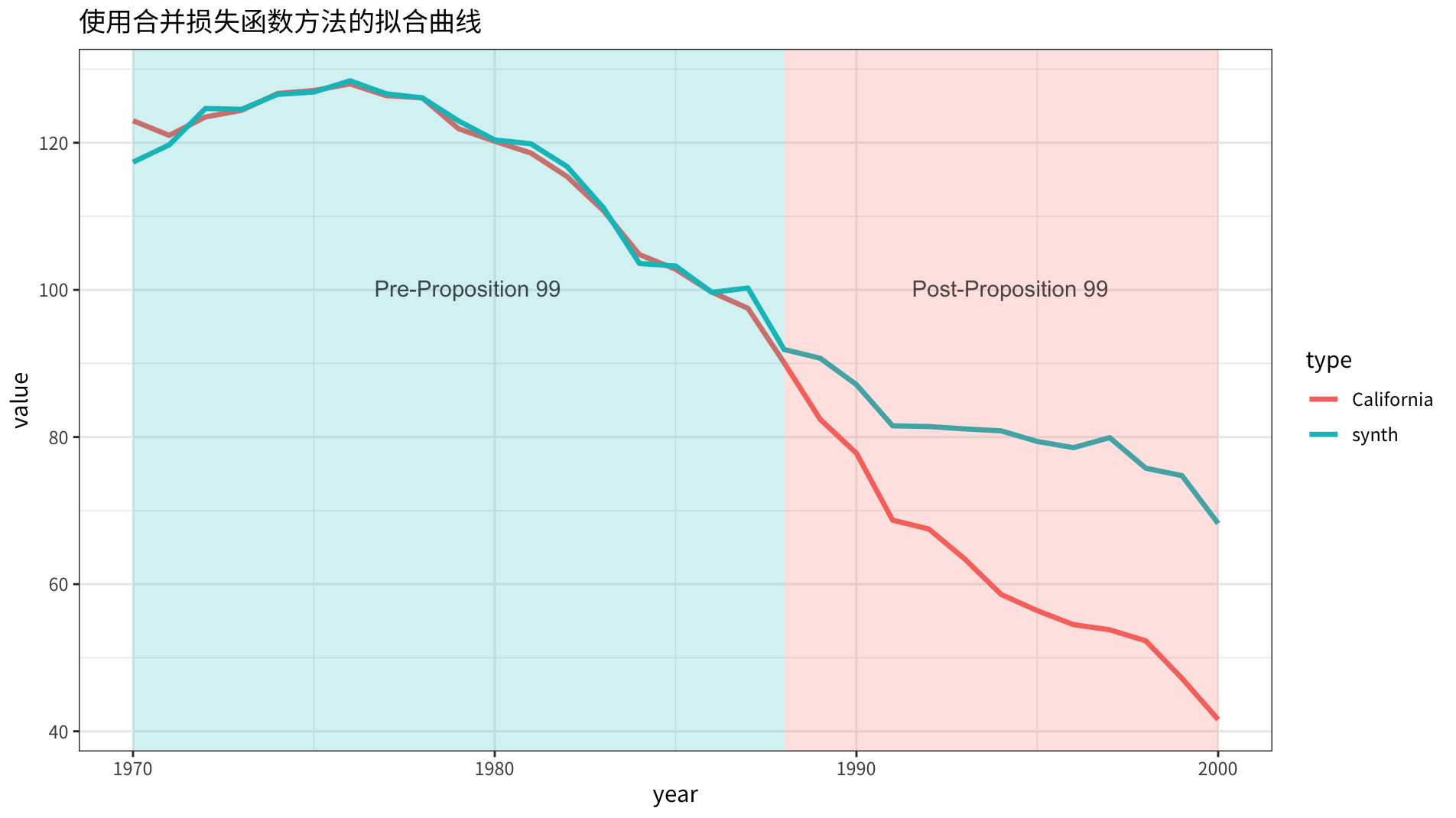
$\lambda = 0.01$ 时，这个结果更倾向于协变量的拟合，可以看到：合成的协变量向量，除 lnincome 外，几乎完全一致。

合成的 $\hat{Y}_{1t}$ 同原始 $Y_{1t}$ 的对比曲线如下图所示：

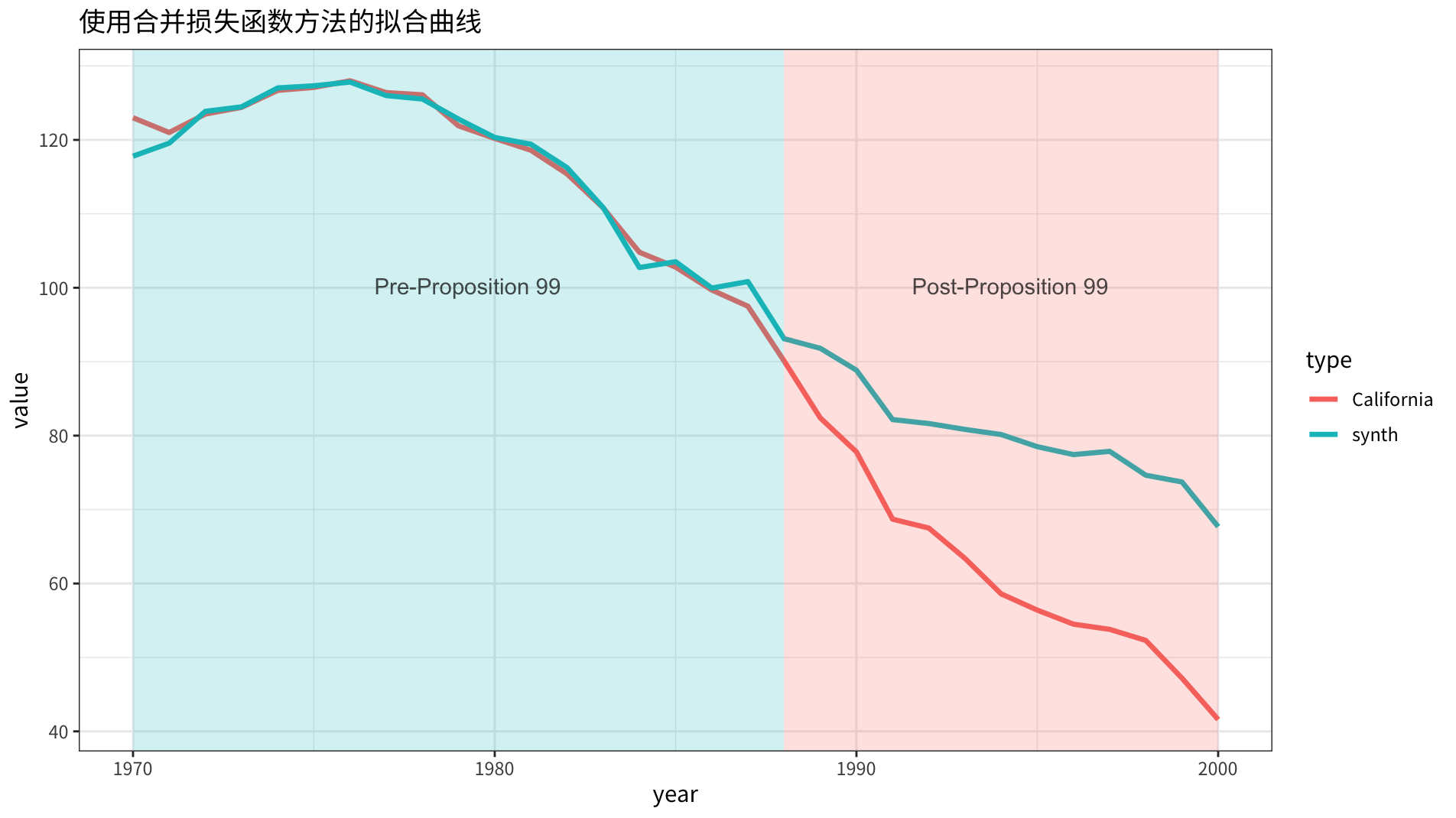
从结果变量的拟合结果上看，两者有细微的差别。因为权重低，整体表现要比 $\lambda=1$ 时要差一些。

5. 同时做变量选择

设想以下需求场景：

• 假如观测的段 $T$ 为 20，但是对照单元 $J$ 为 1000，那么合成控制组的构建会变得非常困难。在这种情况下，我们需要尽可能压缩权重向量 $w$，以简化合成控制组的构建。
• 前文提到的方法是最小化 $Z_1 - Z_0 W$ 的平方误差，但如果模型过拟合怎么办？泛化能力过弱怎么办？

当然，这个想法是有代价的，不可能既要又要还要。这时需要酌情放宽 $w$ 的限制条件，不再要求 $\sum_{j=2}^{J+1} w_j = 1$ 且 $w_j \geq 0$ 这两个条件。

5.1. 具体实现过程

在合成控制法中，我们更关注的是结果变量 $Y$ 的拟合，而协变量 $X$ 主要用于辅助构建合成控制组。通过权重 $\lambda, V$ 将 $Y$ 和 $X$ 合并成为一个统一的响应变量，并使用权重向量 $\mathbf{w}$ 来构建合成控制组。

假设我们有 $J+1$ 个单元，其中第 1 个单元是处理单元，其余 $J$ 个单元是对照单元。我们观测到每个单元在 $T$ 个时间段内的结果变量 $Y$ 和协变量 $X$。

定义：

• $Y_{it}$：单元 $i$ 在时间 $t$ 的结果变量。
• $X_{i}$：单元 $i$ 的协变量向量。
• $\lambda$ 正则化参数，用于平衡结果变量和协变量的拟合程度。
• $V$ 协变量的权重矩阵，用于调整协变量的重要性。

可以将 $Y$ 和 $X$ 视为一个扩展的响应变量向量 $\mathbf{z}_{it}$，其中 $\mathbf{z}_{it}$ 包含 $Y_{it}$ 和 $X_{i}$，表示为：

然后，我们可以定义一个新的目标函数，将 $Y$ 和 $X$ 合并在一起：

其中，$\mathbf{z}_{1t}$ 是处理单元在时间 $t$ 的扩展响应变量，$\mathbf{z}_{jt}$ 是对照单元 $j$ 在时间 $t$ 的扩展响应变量。

这个目标函数包含两个部分：

1. 扩展响应变量的平方误差项。
2. L1 正则化项。

这种方式将 $Y$ 和 $X$ 合并在一起，并使用类似 LASSO 的方法来求解权重 $\mathbf{w}$。在这个框架下，我们就可以采用交叉验证的方法来选择 MSE 效果最好的参数来构建模型，也可以更灵活地处理结果变量和协变量的关系，同时进行变量选择和系数收缩。

5.2. 转化为弹性网络问题

也可以将它改写成 Elastic Net 模型形式：

其中的超参数 $\alpha$ 和 $\lambda$ 通过交叉验证的机器学习框架，求解泛化能力最好，且能让 loss 最小的 $w$。

5.3. 系数和模型结果

需要注意的是，这种方法很灵活，不需要协变量为面板数据。

            X_synth    X1
lnincome      0.131 0.164
beer          0.145 0.161
age15to24     0.128 0.160
retprice      0.130 0.165
cigsale1975   0.141 0.144
cigsale1980   0.135 0.137
cigsale1988   0.127 0.125

合成的 $\hat{Y}_{1t}$ 同原始 $Y_{1t}$ 的对比曲线如下图所示：

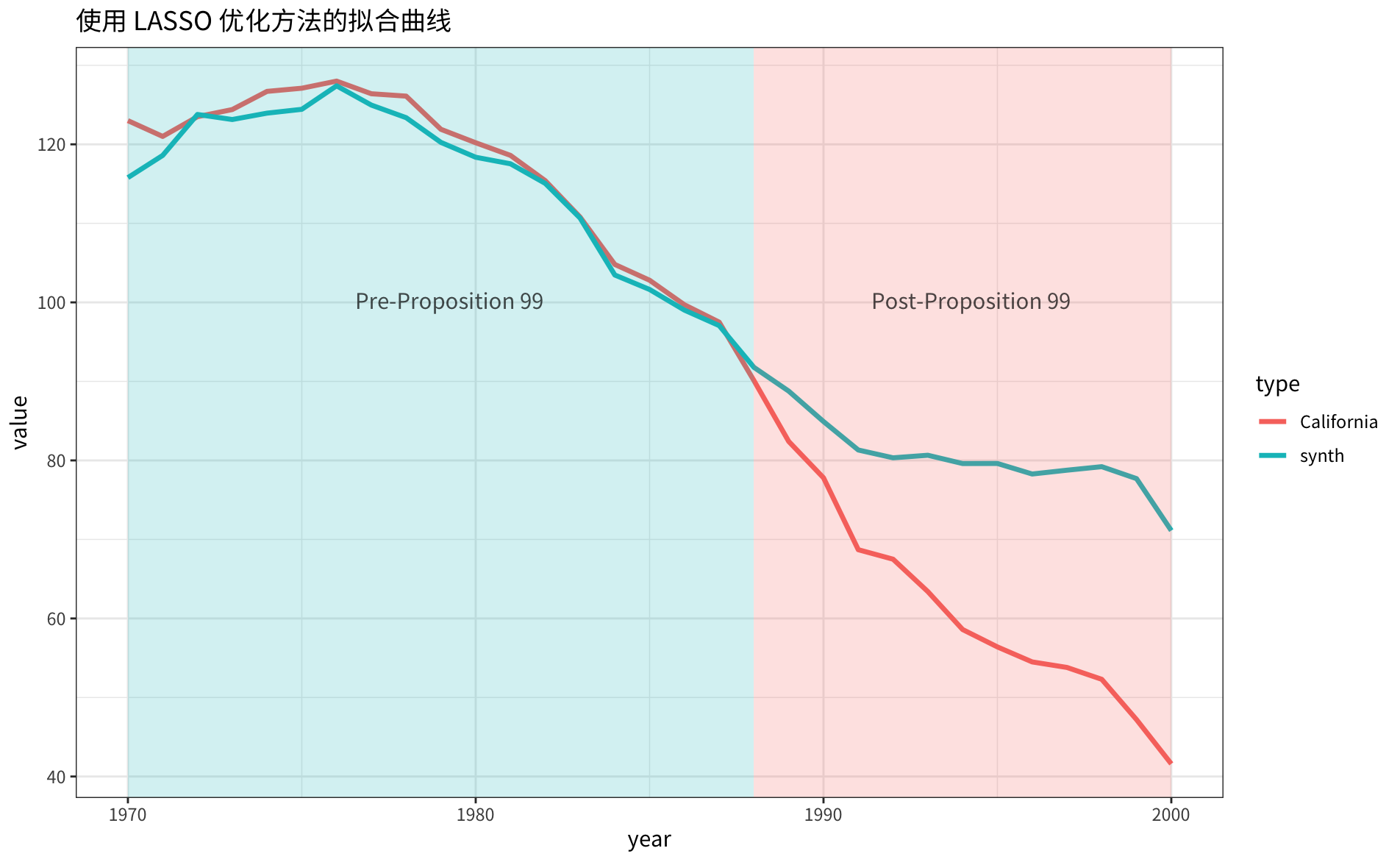
虽然从拟合曲线上比前面的两种方法表现都要差，但我个人还是更加认可这个方法，毕竟通过交叉验证的参数，泛化性更好，结果更加稳健。

当然如果你只关注结果变量 $Y_i$ 的拟合程度，而不想考虑协变量 $X_i$ 的影响。恭喜你，你发现了一种新的方法——SDID。

6. 总结

本文注意力主要集中在如何更便捷的求解合成控制法中的参数，并没有更多的讨论安慰剂检验等其他细节。合成控制法是一个非常好的，用于估计政策或活动影响变化的框架。算法细节上使用嵌套优化的方法，非常优雅。但它也有一定局限性，有改进的可能：

1. 使用嵌套完全最优化的方法可能会出现过拟合的情况，模型存在稳定性问题，不利于估计因果效用。
2. 合并损失的方式是可行方法之一，可以控制输出变量和协变量的权重。但需要留意，$X$ 和 $Y$ 都要做归一化处理。
3. 引入全新的损失函数，增加正则项，借助通用机器学习框架，可以解决权重 $w$ 维度过高，以及提升模型的稳健性。

注：三个方法实现的 R 代码 1000 多行，太长，先不贴到原文了。