矩阵分解技术是推荐系统常用的技术之一，它的变种出现在很多算法都有涉及。这里先不做展开，对于最基本的矩阵分解技术做一些原理和代码解释。

1. 矩阵分解的数学原理

首先约定一下符号，对于用户（users）的集合 $U$ ，以及商品的集合 $D$ ，用 $R$ 来表示用户商品信息的共现（ $U \times D$ ）矩阵。我们现在想找出 K 个潜在的特征，即：找到两个新矩阵P（ $U \times K$ ），Q（ $D \times K$ ），使得：

$R = P \times Q^T = \hat{R}$

这时，P包含了所有的用户（U）的相关信息（特征），而 Q 则包含了商品的相关信息（特征）。那如何找到这两个矩阵呢？

其中的一种方法就是梯度下降（gradient descent）：首先先给 P、Q 一些初始值，然后计算R和 $P \times Q$ 的差异，接着通过迭代最小化二者的差异。这个差异我们一般用如下的方式表示：

\begin{equation} e_{ij}^2 = (r_{ij} - \hat{r}_{ij})^2 \end{equation}

\begin{equation} = (r_{ij} - \sum_{k=1}^K p_{ik} q_{kj})^2 \end{equation}

对于上式，我们必须找到一个方向来优化 $p_{ik},q_{kj}$ 。换句话说，我们需要知道当前值的梯度下降方向：

$\frac{\partial e_{ij}^2}{\partial p_{ik}}=-2(r_{ij}-\hat{r}_{ij})(q_{kj})=-2e_{ij}q_{kj}$

$\frac{\partial e_{ij}^2}{\partial q_{ik}} = -2(r_{ij} - \hat{r}_{ij})(p_{ik}) = -2 e_{ij}p_{ik}$

既然以及找到梯度，那则有

$p_{ik}^{new} = p_{ik} + 2\alpha e_{ij} q_{kj}$

$q_{kj}^{new} = q_{kj} + 2\alpha e_{ij} p_{ik}$

这里 $\alpha$ 是一个常数，决定梯度的步长，为了避免越过局部最优值，所以 $\alpha$ 一般都是一个很小的数，比如0.0002。

另外一个问题有来了：

如果我们求得的 P 和 Q 的乘积同 R 完全一致，那么未观测的值（表示为零的行为），依旧是零。

这里需要澄清一下：我们只对原始数据不为零的元素求解二者差异，而不是全部的元素。

2. 正则化 Regularization

为了避免过拟合，我们一般会引入 Regularization 来作为惩罚项，一般是引入一个 $\beta$ 来修改误差的平方：

\begin{equation} e_{ij}^2 = (r_{ij} - \sum_{k=1}^K p_{ik} q_{kj})^2 + \frac{\beta}{2} \sum_{k=1}^K(||P||^2 + ||Q||^2) \end{equation}

$\beta$ 用来控制用户特征和商品特征的程度（magnitudes），保证 P、Q 对 R 的近似，但不会出现太大的数值。

这样梯度下降的规则就变成了如下：

$p_{ik}^{new} = p_{ik} + 2\alpha e_{ij} q_{kj} - \beta p_{ik}$

$q_{kj}^{new} = q_{kj} + 2\alpha e_{ij} p_{ik} - \beta q_{kj}$

3. 上代码

为了简化，我将 $Q^T$ 直接写成了 $Q$ 。


steps <- 1000 # the maximum number of steps to perform the optimisation
alpha <- 0.0002 # the learning rate
beta <- 0.02 # the regularization parameter
K <- 3  # the number of latent features

R <- as.matrix(read.csv(textConnection("
0 0 3 3 0 0 0
0 0 1 0 2 0 0
0 1 2 0 0 0 0
0 0 0 0 2 0 2
0 3 0 0 0 4 0
0 2 0 3 0 2 0
3 0 0 0 0 0 2
0 0 5 0 0 3 0
"), header = FALSE, sep = ' '))

m <- nrow(R)
n <- ncol(R)
P <- matrix(rnorm(m * K, 0, .5), m, K, byrow = T)
Q <- matrix(rnorm(n * K, 0, .5), K, n, byrow = T)
print(P)
print(Q)

eij <- numeric(1)
loss <- numeric(1)

for(s in 1:steps){
    for(i in 1:m){
        for(j in 1:n){
            if (R[i,j] > 0) eij <- R[i,j] - P[i,] %*% Q[,j]
            for(k in 1:K){
                P[i,k] <- P[i,k] + alpha * (2 * eij * Q[k,j] - beta * P[i,k])
                Q[k,j] <- Q[k,j] + alpha * (2 * eij * P[i,k] - beta * Q[k,j])
            }
        }
    }
    e <- 0
    for(i in 1:m){
        for(j in 1:n){
            if (R[i,j] > 0) e <- (R[i,j] - P[i,]%*%Q[,j])^2
        }
    }
    loss[s] <- e
}

library(ggplot2)
ggplot(data.frame(s = 1:length(loss), loss), aes(x = s, y = loss)) + geom_line()
round(P %*% Q, 1)
R

我们先看一下每一步迭代后的损失

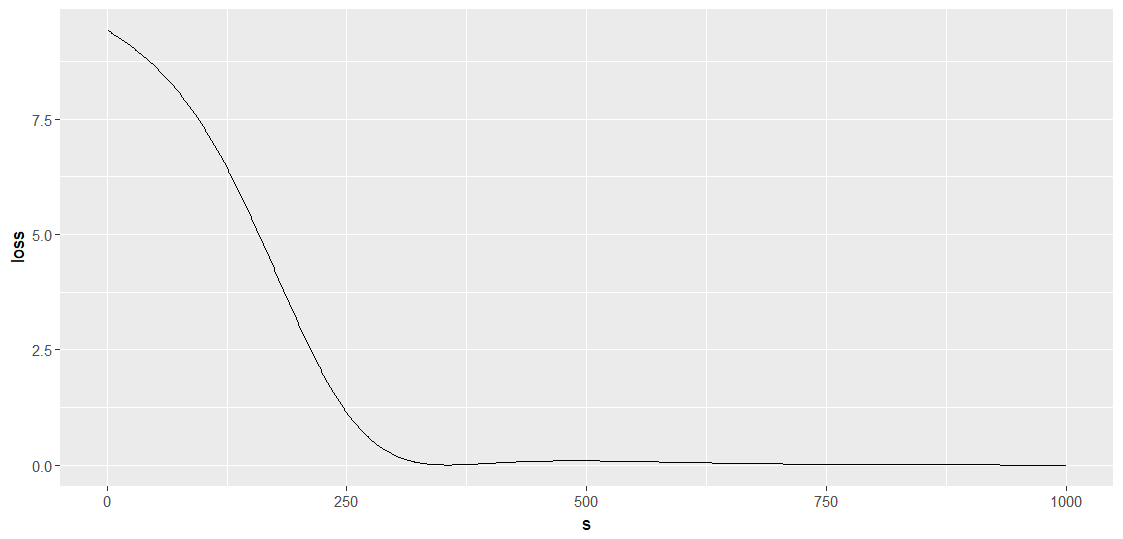
客官会看到损失在后面有提高，如何规避请自行思考。

对比一下结果（因为随机初始化的 P 和 Q，所以我们的结果肯定不一样）：

> round(P %*% Q, 2)
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 4.07 2.24 2.78 3.01 3.83 2.76 3.13
[2,] 1.16 0.07 1.21 1.74 1.84 0.62 0.83
[3,] 2.46 1.21 2.04 2.20 2.77 1.59 1.90
[4,] 2.15 1.00 1.46 1.79 2.11 1.42 1.61
[5,] 5.98 3.00 4.82 5.22 6.57 3.90 4.63
[6,] 3.35 1.78 3.04 3.04 3.99 2.16 2.65
[7,] 3.01 1.38 0.44 1.51 1.26 2.20 2.05
[8,] 5.04 1.68 4.99 5.92 6.98 3.00 3.85
> R
     V1 V2 V3 V4 V5 V6 V7
[1,]  0  0  3  3  0  0  0
[2,]  0  0  1  0  2  0  0
[3,]  0  1  2  0  0  0  0
[4,]  0  0  0  0  2  0  2
[5,]  0  3  0  0  0  4  0
[6,]  0  2  0  3  0  2  0
[7,]  3  0  0  0  0  0  2
[8,]  0  0  5  0  0  3  0

4. 其他

生产环境肯定不会这样存储数据的，不同的存储方式在计算逻辑上会大有不同。
初始化 P 和 Q 的策略不同，会导致收敛速度和结果不同。
$\alpha$ 和 $\beta$ 的设置不同会导致收敛速度不一致，是否可以动态调整，答案是，请自行搜索。